75: Redis new data structure: the HyperLogLog Back
origin: http://antirez.com/news/75
Generally speaking, I love randomized algorithms, but there is one I love particularly since even after you understand how it works, it still remains magical from a programmer point of view. It accomplishes something that is almost illogical given how little it asks for in terms of time or space. This algorithm is called HyperLogLog, and today it is introduced as a new data structure for Redis.
Counting unique things
Usually counting unique things, for example the number of unique IPs that connected today to your web site, or the number of unique searches that your users performed, requires to remember all the unique elements encountered(遇見的) so far, in order to match the next element with the set of already seen elements, and increment a counter only if the new element was never seen before.
This requires an amount of memory proportional(等比例的) to the cardinality(基數)(number of items) in the set we are counting, which is, often absolutely prohibitive(过高的).
There is a class of algorithms that use randomization in order to provide an approximation(近似值) of the number of unique elements in a set using just a constant, and small, amount of memory. The best of such algorithms currently known is called HyperLogLog, and is due to Philippe Flajolet.
HyperLogLog is remarkable(非凡的) as it provides a very good approximation of the cardinality of a set even using a very small amount of memory. In the Redis implementation it only uses 12kbytes per key to count with a standard error of 0.81%, and there is no limit to the number of items you can count, unless you approach 2^64 items (which seems quite unlikely).
The algorithm is documented in the original paper 1(http://algo.inria.fr/flajolet/Publications/FlFuGaMe07.pdf), and its practical implementation and variants were covered in depth by a 2013 paper from Google 2(http://static.googleusercontent.com/media/research.google.com/en//pubs/archive/40671.pdf).
How it works?
There are plenty of wonderful resources to learn more about HyperLogLog, such as 3(http://blog.aggregateknowledge.com/2012/10/25/sketch-of-the-day-hyperloglog-cornerstone-of-a-big-data-infrastructure/).
Here I'll cover only the basic idea using a very clever example found at 3(http://blog.aggregateknowledge.com/2012/10/25/sketch-of-the-day-hyperloglog-cornerstone-of-a-big-data-infrastructure/). Imagine you tell me you spent your day flipping a coin(用手指頭往上彈硬幣), counting how many times you encountered a non interrupted run of heads. If you tell me that the maximum run was of 3 heads, I can imagine that you did not really flipped the coin a lot of times. If instead your longest run was 13, you probably spent a lot of time flipping the coin.
However if you get lucky and the first time you get 10 heads, an event that is unlikely but possible, and then stop flipping your coin, I'll provide you a very wrong approximation of the time you spent flipping the coin. So I may ask you to repeat the experiment, but this time using 10 coins, and 10 different piece of papers, one per coin, where you record the longest run of heads. This time since I can observe more data, my estimation will be better.
Long story short this is what HyperLogLog does: it hashes every new element you observe. Part of the hash is used to index a register(寄存器) (the coin+paper pair, in our previous example. Basically we are splitting the original set into m subsets). The other part of the hash is used to count the longest run of leading zeroes in the hash (our run of heads). The probability of a run of N+1 zeroes is half the probability of a run of length N, so observing the value of the different registers, that are set to the maximum run of zeroes observed so far for a given subset, HyperLogLog is able to provide a very good approximated cardinality.
The Redis implementation
The standard error of HyperLogLog is 1.04/sqrt(m), where “m” is the number of registers used.
Redis uses 16384 registers, so the standard error is 0.81%.
Since the hash function used in the Redis implementation has a 64 bit output, and we use 14 bits of the hash output in order to address our 16k registers, we are left with 50 bits, so the longest run of zeroes we can encounter will fit a 6 bit register. This is why a Redis HyperLogLog value only uses 12k bytes for 16k registers.
Because of the use of a 64 bit output function, which is one of the modifications of the algorithm that Google presented in 2(http://static.googleusercontent.com/media/research.google.com/en//pubs/archive/40671.pdf), there are no practical limits to the cardinality of the sets we can count. Moreover it is worth to note that the error for very small cardinalities tend to be very small. The following graph shows a run of the algorithm against two different large sets. The cardinality of the set is shown in the x axis, while the relative error (in percentage) in the y axis.
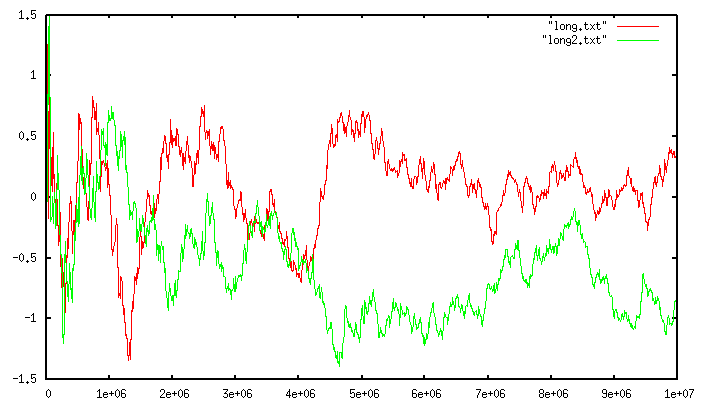
The red and green lines are two different runs with two totally unrelated sets. It shows how the error is consistent(一致的) as the cardinality increases. However for much smaller cardinalities, you can enjoy a much smaller error:
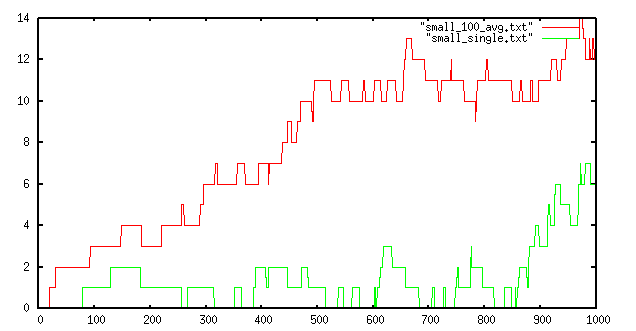
The green line shows the error of a single run up to cardinality 100, while the red line is the maximum error found in 100 runs. Up to a cardinality of a few hundreds the algorithm is very likely to make a very small error or to provide the exact answer. This is very valuable when the computed value is shown to an user that can visually match if the answer is correct.
The source code of the Redis implementation is available at Github: The source code of the Redis implementation is available at Github:
The API
From the point of view of Redis an HyperLogLog is just a string, that happens to be exactly 12k + 8 bytes in length (12296 bytes to be precise). All the HyperLogLog commands will happily run if called with a String value exactly of this size, or will report an error. However all the calls are safe whatever is stored in the string: you can store garbage and still ask for an estimation(估值) of the cardinality. In no case this will make the server crash.
Also everything in the representation is endian(字節順序) neutral and is not affected by the processor word size, so a 32 bit big endian processor can read the HLL of a 64 bit little endian processor.
The fact that HyperLogLogs are strings avoided the introduction of an actual type at RDB(關係型數據庫) level. This allows the work to be back ported into Redis 2.8 in the next days, so you'll be able to use HyperLogLogs ASAP (as soon as possible). Moreover the format is automatically serialized, and can be retrieved and restored easily.
The API is constituted of three new commands:
PFADD var element element … element
PFCOUNT var
PFMERGE dst src src src … src
The commands prefix is “PF” in honor of Philippe Flajolet 4(http://en.wikipedia.org/wiki/Philippe_Flajolet).
PFADD adds elements to the HLL (HyperLogLog) stored at “var”. If the variable does not exist, an empty HLL is automatically created as it happens always with Redis API calls. The command is variadic(可變的), so allows for very aggressive pipelining(流水線) and mass(大量的) insertion.