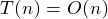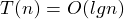Heap Sort Back
Overview
- 堆排序: 利用大頂堆或小頂堆的特性, 每趟取出樹根結點並調整堆, 直到所有數被取出.
- 大頂堆:
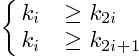
- 小頂堆:
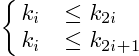
- 时间复杂度:
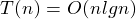 (最好,平均,最壞情況)
(最好,平均,最壞情況)
- 空間複雜度:

- 稳定性: 不稳定
- 适用情况: 實時應用, 快速取出最大或最小值
- BUILD_MAX_HEAP:
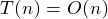
- MAX_HEAPIFY:
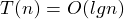
Example
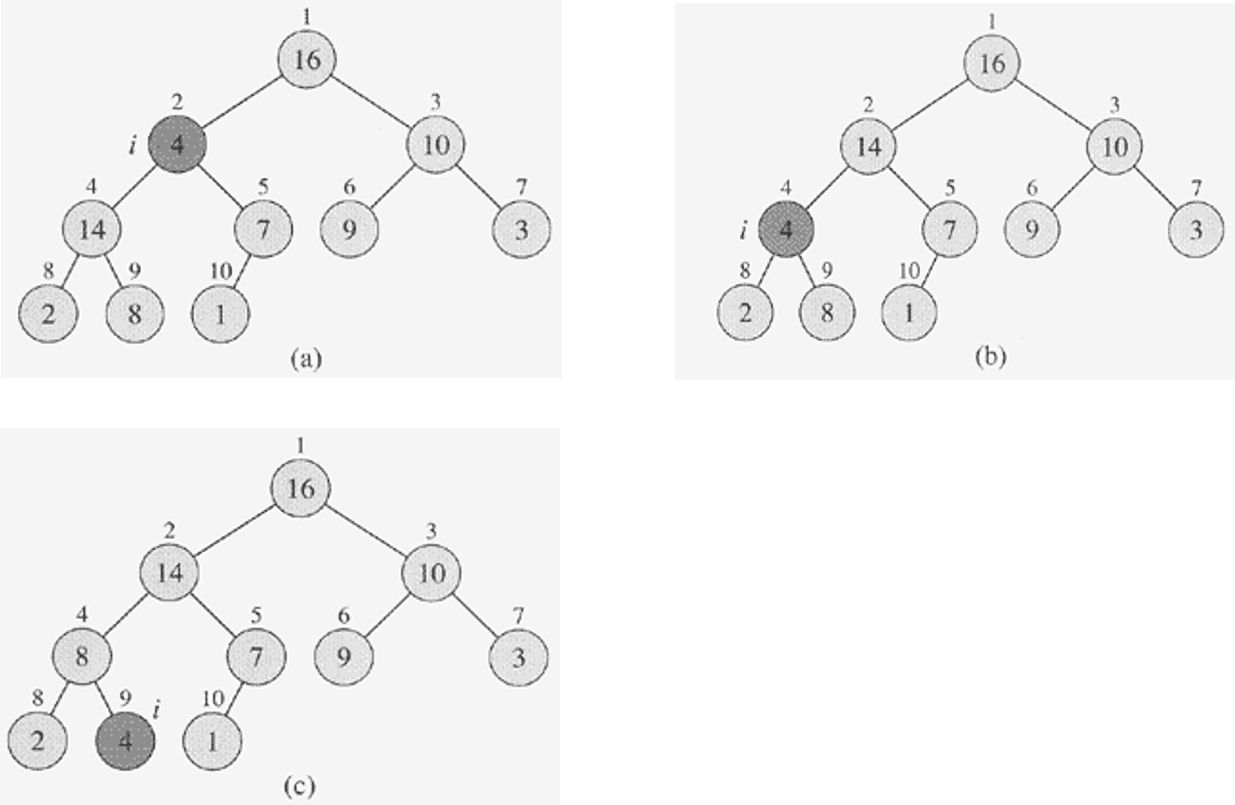
1. BUILD_MAX_HEAP
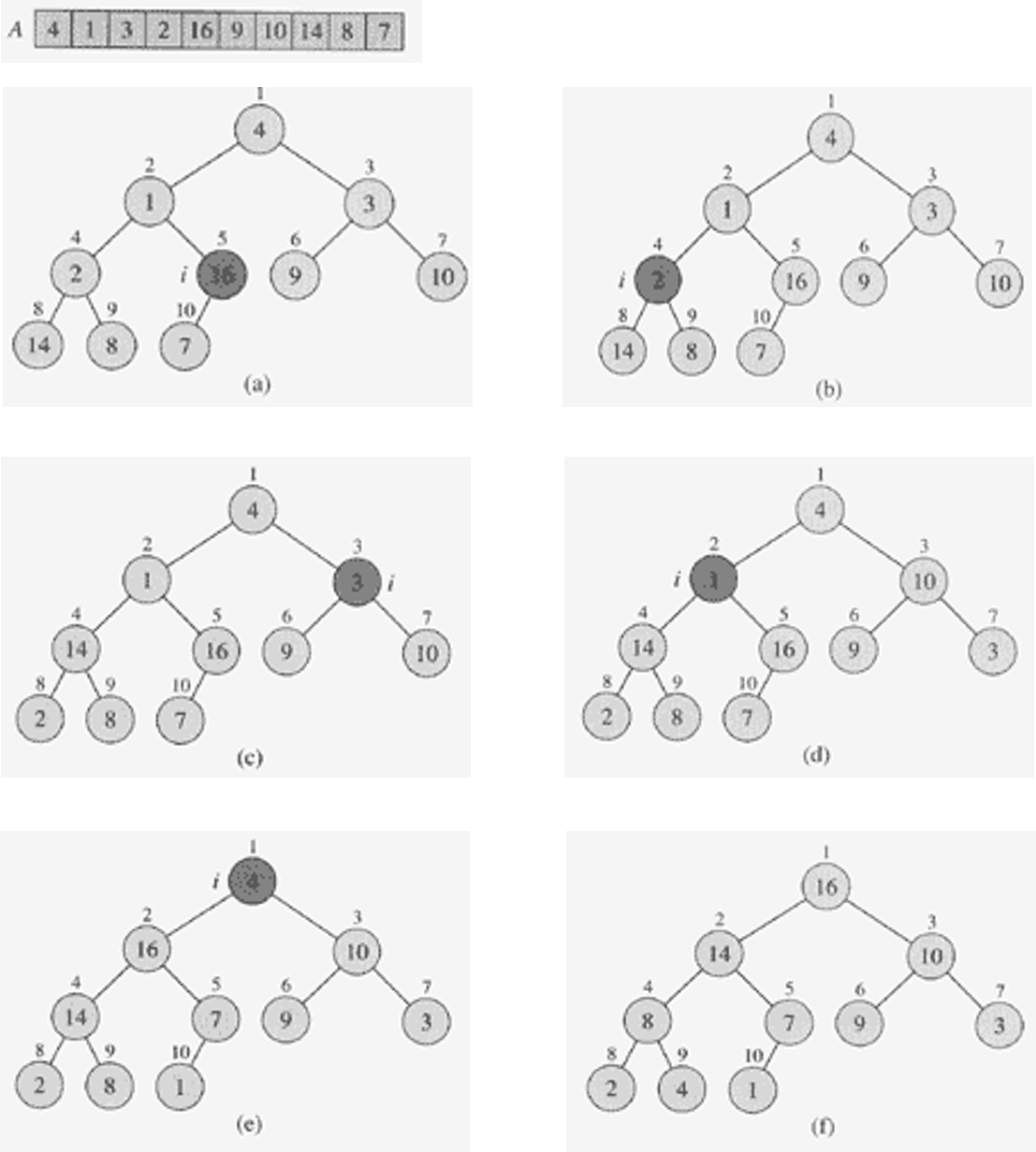
2. MAX_HEAPIFY
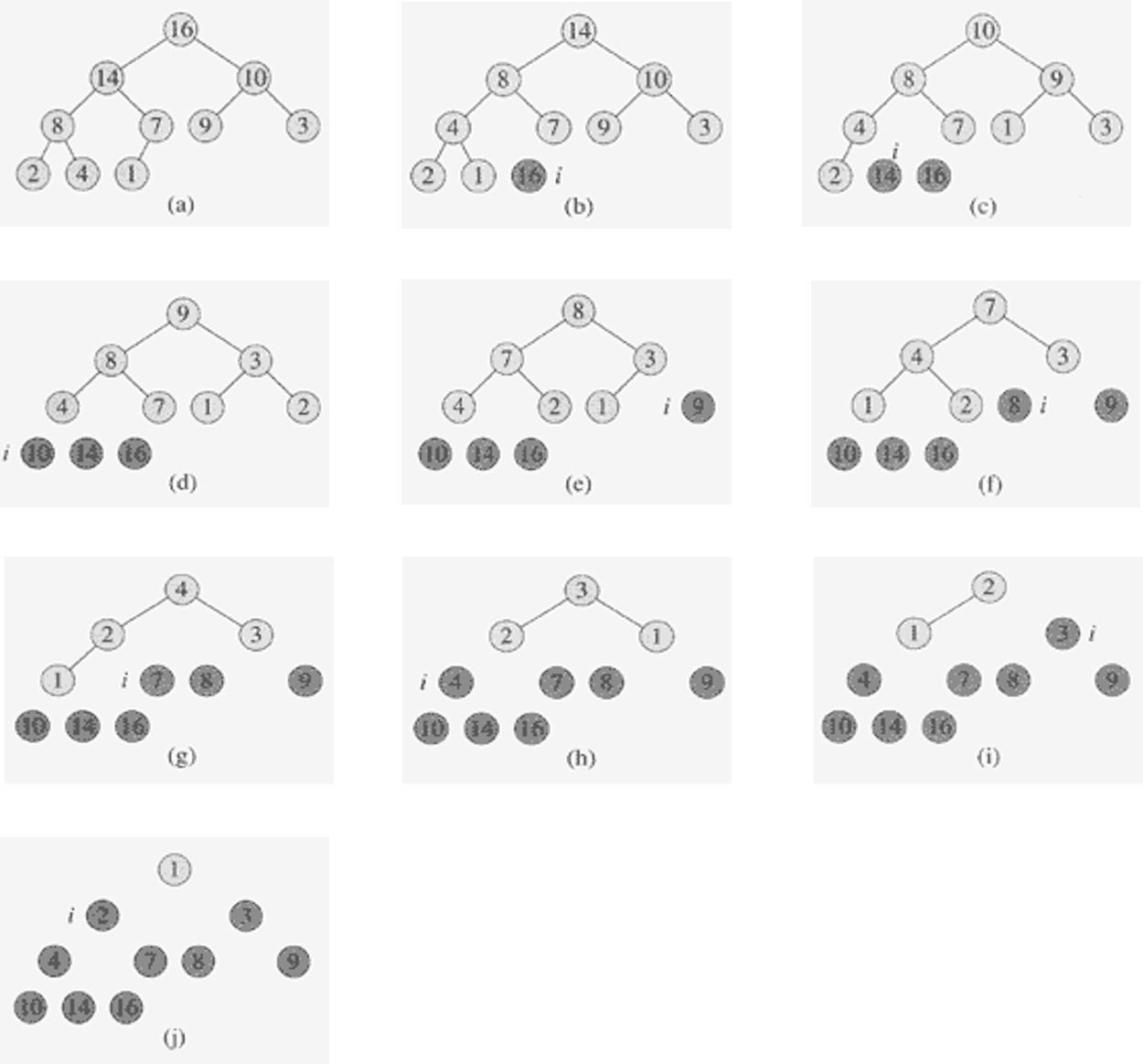
3. HEAP_SORT
Code
void MAX_HEAPIFY(int A[], int heap_size, int i)
{
int largest;
int l = LEFT(i);
int r = RIGHT(i);
if (l < heap_size && A[l] > A[i])
largest = l;
else
largest = i;
if (r < heap_size && A[r] > A[largest])
largest = r;
if (largest != i)
{
exchange(A, i, largest);
MAX_HEAPIFY(A, heap_size, largest);
}
}
void BUILD_MAX_HEAP(int A[], int heap_size)
{
for (int i = heap_size / 2 - 1; i >= 0; i--)
MAX_HEAPIFY(A, heap_size, i);
}
void HEAPSORT(int A[], int* heap_size)
{
BUILD_MAX_HEAP(A,*heap_size);
for (int i = *heap_size - 1; i > 0; i--)
{
exchange(A, 0, i);
*heap_size = *heap_size - 1;
MAX_HEAPIFY(A, *heap_size, 0);
}
}
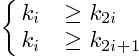
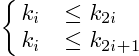
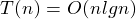 (最好,平均,最壞情況)
(最好,平均,最壞情況)